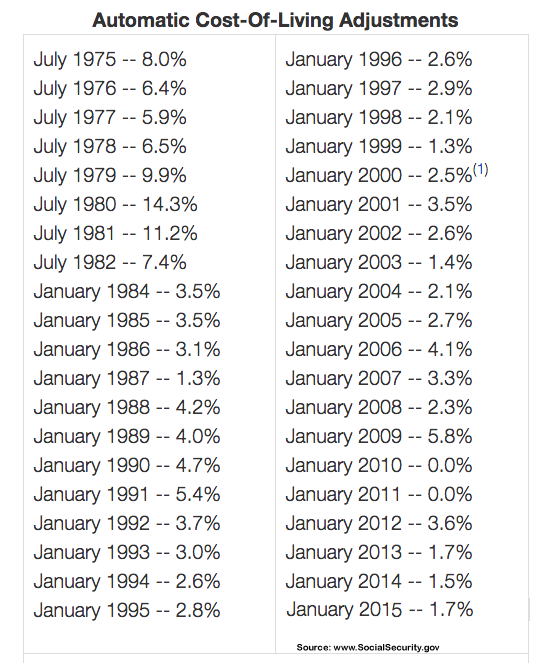
Longevity Annuities are one of the simplest and low cost annuities to understand and own. Give a deposit to the insurance company in return for a guaranteed income at your selected date in the future that must be greater than twelve months from deposit. July 2nd 2014 the US Treasury Department made law in the Federal Registry a QLAC (Qualified Longevity Annuity Contract). This “qualified” longevity annuity was now tax favored. The main benefit of the QLAC is to allow IRA owners the ability to delay the required minimum distribution (RMD) requirement to past age 70 ½ and not have to pay taxes on that distribution until up to age 85 if selected. Some details of the requirements to become a QLAC:
– 25% of any 401k, Defined benefit, 457b, Pension Plan, or 403b also 25% across all pre-tax IRAs, excluding Roth IRA, aggregated together can be invested into a QLAC. That 25% balance is as of December 31st of the prior calendar year.
– The cumulative dollar amount invested into QLACs across all retirement accounts may NOT exceed the LESSER of $125,000 or 25% above balance threshold.
– The QLAC must begin income payments at the latest by age 85.
– The $125,000 dollar amount will be indexed for inflation, CPI, adjusted in $10,000 increments.
– The QLAC must provide fixed income payouts; COLA (cost-of-living adjustment) increases are an approved option.
– The QLAC can have an optional “return of deposit” death benefit option before the income start date and also have a return of deposit death benefit after income starts. Installment refunds or lump sum death benefits are the two options available.
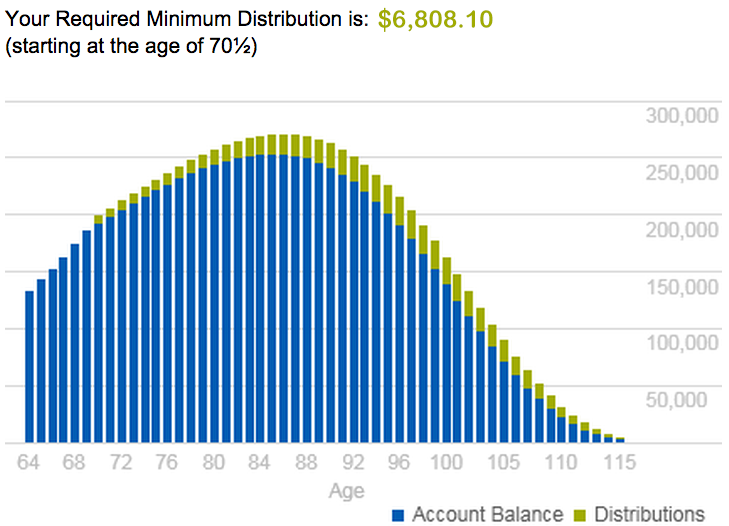
By not having to take the required minimum distribution (RMD) every year after age 70 ½ until age 85 gives the QLAC owner huge tax savings. Lets take a look at an example of a 65 year old purchasing a QLAC this year and starting income at age 85. If the QLAC owner has the maximum IRA balance of $500,000 the prior year then she can invest the maximum limit into a QLAC of $125,000. To compare what the tax savings would be to a QLAC owner the $125,000 balance would be invested into a stock-like investment inside an IRA getting an annual return of 6.9% for this example. At age 70 ½ that initial $125,000 investment would grow to $192,605 and the RMD would be $6,808 for that year. $6,808 RMD taxed at 28% ordinary income tax rate is $1,906.24 due. The next year at age 71 that initial $125,000 investment would grow to $198,627, after taking the previous years RMD of $6,808, this year’s RMD would be $7,268. $7,268 RMD taxed at 28% ordinary income tax rate is $2,035.04 due. This calculation goes on every year until age 85 when the QLAC income payments start. In the example of the 65 year old who deposit $125,000 into a qualified longevity annuity contract will not pay $46,271 in forced RMD taxes for the years 70 ½ until age 85 by transferring that money into a QLAC.
Income please?
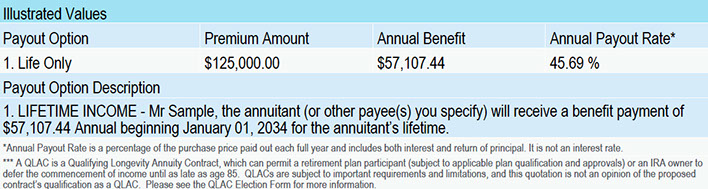
Lets not forget about the income payments a longevity annuity contract holder will receive at the income-selected age. In this example it would be age 85. $125,000 deposit into a QLAC delayed income for twenty years would provide $57,107 annually lifetime income at age 85. That is a 45% annual payout rate and a total income payment if the annuitant lived to age 100 of $913,719.
How to use this annuity in retirement planning?
Transferring retirement dollars over to the QLAC saves your income tax dollars for many years as the example above showed. It also gives constant lifetime income to cover your basic expenses later in retirement. Investment research studies have shown that converting a small portion, less than 50%, of your retirement funds to a longevity income annuity such as a QLAC will increase your portfolio income success rate over a 20-year time frame. By eliminating stock market risk with a purchase of a QLAC will produce lifetime income in retirement that cannot be outlived.